Elliptic Curves
The original Sato-Tate conjecture wasn't about modular forms, but about a class of geometric objects called elliptic curves. These curves are defined by equations similar to the following: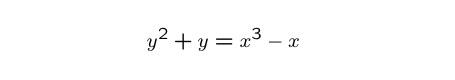
| p | N(p) | ap | |ap|p-1/2 |
| 2 | 2 | 0 | 0 |
| 3 | 3 | 0 | 0 |
| 5 | 7 | -2 | 0.89 |
| 7 | 7 | 0 | 0 |
| 11 | 11 | 0 | 0 |
| 13 | 7 | 6 | 1.66 |
| 17 | 15 | 2 | 0.49 |
| 19 | 19 | 0 | 0 |
| 23 | 23 | 0 | 0 |
| 29 | 39 | -10 | 1.86 |
| 31 | 31 | 0 | 0 |
| 37 | 39 | -2 | 0.33 |

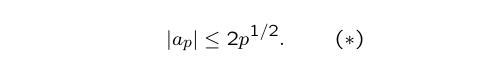
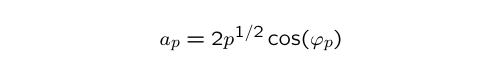
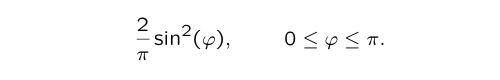
By the celebrated Modularity Theorem, the Sato-Tate conjecture
for elliptic curves is actually a consequence of the Sato-Tate conjecture for modular forms.
Namely, the Modularity Theorem states that the numbers ap defined above for
an elliptic curve are in fact the Fourier coefficients of a modular form (a cuspidal
eigen-newform of weight 2, to be precise). Hence, if we
know the sin2 law for modular forms, we know it for elliptic curves.
We should remark that the modular forms in the Modularity Theorem are not exactly
of the type that we defined on page 2. It is necessary to consider modular forms
with ''level''. For example, the modular form corresponding to the elliptic curve
y2+y=x3-x above is the essentially unique cusp form of weight 2 and level 11.
There is still more - go to page 4.
