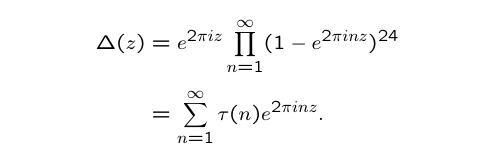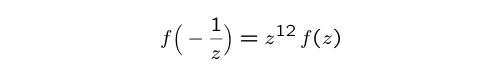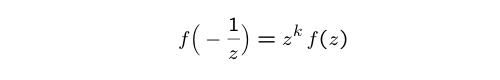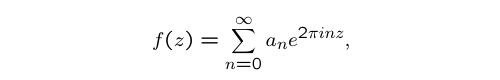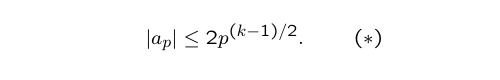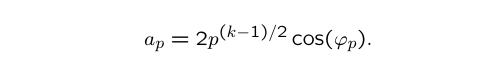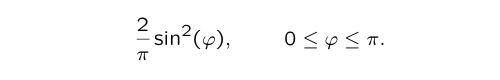Modular forms
Recall the formal product in the variable q we considered above. If we replace
q with exp(2πiz), where z is a complex number, we obtain a function of z,
which is called the
Ramanujan Δ Function
or
discriminant function:
Of course, in order for this product and this sum to converge, we must have
Im(z)>0. In other words, z is an element of the complex upper half plane
consisting of all complex numbers with positive imaginary part. Obviously
Δ has the property that &Delta(z+1)=&Delta(z). One can
show that Δ satisfies the additional transformation property
The number 12 in the exponent is called the
weight.
In general, if k is a positive integer, and if f(z) is a holomorphic function on the
complex upper half plane that satisfies
and that has a
Fourier expansion of the form
then f is called a
modular form of weight k.
The numbers a
n are called the
Fourier coefficients
of f, and if the constant term a
0 is zero, then f is called a
cusp form.
| k | dim Mk | dim Sk |
| 2 | 0 | 0 |
| 4 | 1 | 0 |
| 6 | 1 | 0 |
| 8 | 1 | 0 |
| 10 | 1 | 0 |
| 12 | 2 | 1 |
| 14 | 1 | 0 |
| 16 | 2 | 1 |
| 18 | 2 | 1 |
| 20 | 2 | 1 |
| 22 | 2 | 1 |
| 24 | 3 | 2 |
Hence Δ is a cusp form of weight 12,
and the numbers τ(n) are its Fourier coefficients.
A fundamental result says that the vector space M
k of cusp forms
of weight k is finite-dimensional. Of course, the same is then true for
the subspace S
k of cusp forms. If the Fourier coefficients of a
cusp form f have the property that a
ma
n=a
mn
whenever gcd(m,n)=1, then f is called an
eigenform.
It can be proved that S
k has a vector space basis consisting of
eigenforms.
The Sato-Tate conjecture is actually a statement
for eigen-cuspforms, in the following sense. Let a
n be the
Fourier coefficients of a cusp form of weight k that is also an eigenform.
By Deligne's theorem, we have
Therefore, there exists a Frobenius angle φ
p between 0 and π for which
The Sato-Tate conjecture then asserts that these angles are distributed according to
the same function as before,
The display below demonstrates the Sato-Tate conjecture for the two eigenforms of weight 24.